Welcome to pyTSEB’s documentation!¶
Summary¶
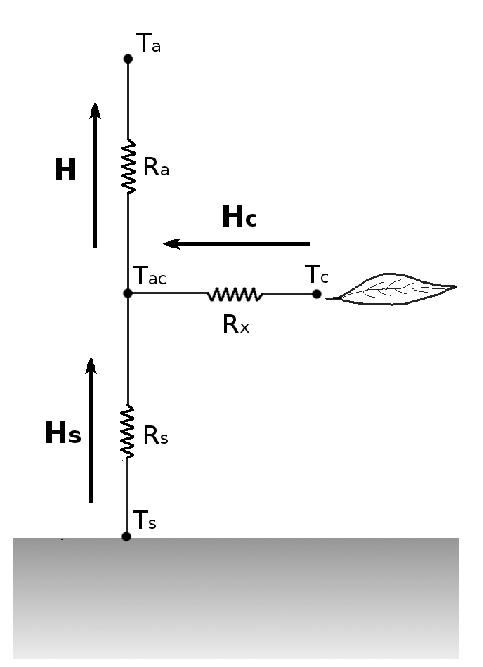
The Two Source Energy Balance (TSEB) model computes the turbulent fluxes for two layers, soil and vegetation, with the interaction between the layers being allowed. Therefore, following an analogy between the flux transport and the Ohm’s Law for transport of electricity, the network of sensible H and latent \(\lambda E\) heat flux transfers can be thought of as being in series and represented as in:
In the TSEB scheme \(\lambda E\) is usually estimated as a residual of the surface energy balance:
with
In the above equations \(\rho_{air}\) is the density of air, \(C_{p}\) is the heat capacity of air at constant pressure, \(T_{AC}\) is the air temperature at the canopy interface:
\(T_C\) and \(T_S\) are related to the directional radiometric temperature \(T_{rad}\left(\theta\right)\) by
with \(f_c\left(\theta\right)\) representing the fraction of vegetation observed by a sensor pointing at a zenith angle \(\theta\)
and \(\kappa_{be}\left(\theta\right)=\frac{\sqrt{\chi^2+\tan^2\theta}}{\chi+1.774\left(\chi+1.182\right)^{-0.733}}\) being the extinction coefficient of a canopy with a leaf angle distribution function defined by the Cambpell 1990 \(\chi\) parameter.
\(r_{a}\), \(r_{x}\) and \(r_{s}\) are the resistances to heat and momentum transfer in the surface layer, from the leaf canopy and from the soil surface respectively.